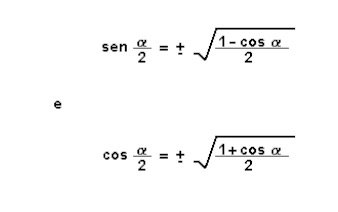Questões de matemática

Origem: Unicamp

(Unicamp-1994) a) Dois círculos concêntricos têm raios 3 e 5 centímetros. Faça um desenho desses círculos de maneira a representar adequadamente seus tamanhos relativos.
b) Desenhe, na figura obtida, e inteiramente contido na região anular interna ao círculo maior e externa ao círculo menor, um segmento de reta de maior comprimento possível.
c) Calcule o comprimento desse segmento.

resposta:Observe as figuras a seguir: (imagem abaixo)
c) AB = 8 cm

(Unicamp-1994) Uma senhora comprou uma caixa de bombons para seus dois filhos. Um destes tirou para si metade dos bombons da caixa. Mais tarde, o outro menino também tirou para si metade dos bombons que encontrou na caixa. Restaram 10 bombons. Calcule quantos bombons havia inicialmente na caixa.

resposta:Havia inicialmente na caixa 40 bombons.

(Unicamp-1994) A divisão de um certo número inteiro positivo N por 1994 deixa resto 148. Calcule o resto da divisão de N+2000 pelo mesmo número 1994.

resposta:O resto é igual a 154.

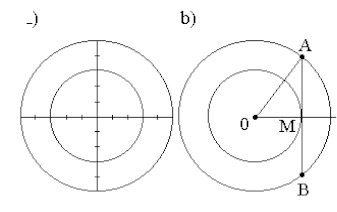
(Unicamp-1994) Uma rampa de inclinação constante, como a que dá acesso ao Palácio do Planalto em Brasília, tem 4 metros de altura na sua parte mais alta. Uma pessoa, tendo começado a subi-la, nota que após caminhar 12,3 metros sobre a rampa está a 1,5 metros de altura em relação ao solo.
a) Faça uma figura ilustrativa da situação descrita.
b) Calcule quantos metros a pessoa ainda deve caminhar para atingir o ponto mais alto da rampa.

resposta:Observe a figura a seguir: (imagem abaixo)
b) 20,5 m

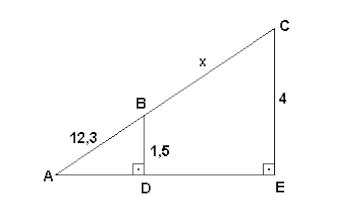
(Unicamp-1994) Em um quadrilátero convexo ABCD, a diagonal AC mede 12 cm e os vértices B e D distam, respectivamente, 3 cm e 5 cm da diagonal AC.
a) Faça uma figura ilustrativa da situação descrita.
b) Calcule a área do quadrilátero.

resposta:a) Observe a figura adiante: (imagem abaixo)
b) S = 48 cm²

(Unicamp-1994) Suponha que todos os preços venham subindo 30% ao mês nos últimos meses e continuem assim nos próximos meses. Calcule:
a) quanto custará, daqui a 60 dias, um objeto que hoje custa CR$ 27.300,00;
b) quanto custava esse mesmo objeto há um mês.

resposta:a) Cr$ 46.137,00
b) Cr$ 21.000,00

(Unicamp-1994) Os números a = 2121 e b = 136 estão escritos nos sistemas de numeração de bases 3 e 7, respectivamente.
a) Como se procede para descobrir qual desses números é o maior≠
b) Determine, então, o maior deles.

resposta:a) Para descobrir qual é o maior número, basta escrevê-los no mesmo sistema de numeração e depois compará-los.
b) O maior número é o b = 76.

(Unicamp-1994) Uma torneira enche um tanque em 12 minutos, enquanto uma segunda torneira gasta 18 minutos para encher o mesmo tanque. Com o tanque inicialmente vazio, abre-se a primeira torneira durante x minutos: ao fim desse tempo fecha-se essa torneira e abre-se a segunda, a qual termina de encher o tanque em x+3 minutos. Calcule o tempo gasto para encher o tanque.

resposta:15 min

(Unicamp-1994) Retiraram x litros de vinho de um barril de 100 litros e adicionam-se, ao mesmo barril, x litros de água. Da mistura resultante no barril, retiram-se outros x litros e adicionam-se outros x litros de água. Agora o barril contém 64 litros de vinho e 36 de água. Calcule o valor de x.

resposta:x = 20

(Unicamp-1994) Determine o quociente e o resto da divisão de x¹(0)(0) + x + 1 por x² - 1.

resposta:quociente: Q(x) = xª⁸ + xª⁶ + ... + x² + 1
resto: R(x) = x + 2

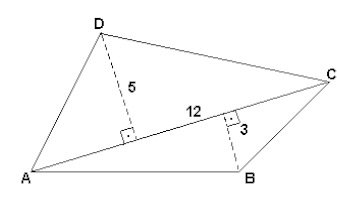
(Unicamp-1994) a) Utilize a fórmula sen²α+cos²α=1 e a fórmula do cosseno da soma de dois ângulos para deduzir as seguintes fórmulas do arco metade: (imagem abaixo)
b) Especifique os intervalos de variação de α nos quais se deve usar o sinal "mais" e nos quais se deve usar o sinal "menos" em cada uma das fórmulas acima.

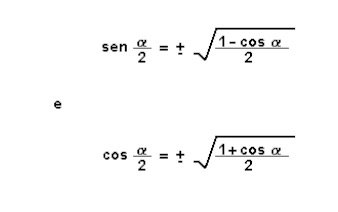resposta:a) Como cos (a + b) = cos a cos b - sen a sen b
e
2a = a + a
temos:
cos (a + a) = cos a cos a - sen a sen a Ì
cos (2a) = cos² a - sen² a (I)

Tomando sen² (α/2) + cos² (α/2) = 1, vem:
{sen² (α/2) = 1 - cos² (α/2) (II)
þ
ÿcos² (α/2) = 1 - sen² (α/2) (III)

Fazendo a = α/2 e substituindo (II) e (III) em (I), encontramos:
{sen (α/2) = √[(1 - cosα)/2]
þ
ÿcos (α/2) = √[(1 + cosα)/2]

b) sen (α/2) tem sinal positivo quando:
0 + 2kπ(Pi) < (α/2) < π(Pi) + 2kπ(Pi), k

Z Ì
4kπ(Pi) < α < (4k + 2)π(Pi), k

Z.

sen (α/2) tem sinal negativo quando:
π(Pi) + 2kπ(Pi) < (α/2) < 2π(Pi) + 2kπ(Pi), k

Z Ì
(4k - 2)π(Pi) < α < (4k + 4)π(Pi), k

Z.

cos (α/2) tem sinal positivo quando:
- (π(Pi)/2) + 2kπ(Pi) < (α/2) < π(Pi)/2 + 2kπ(Pi), k

Z Ì
(4k - 1)π(Pi) < α < (4k + 1)π(Pi), k

Z.

cos (α/2) tem sinal negativo quando:
(π(Pi)/2) + 2kπ(Pi) < (α/2) < (3π(Pi)/2) + 2kπ(Pi), k

Z Ì
(4k + 1)π(Pi) < α < (4k + 3)π(Pi), k

(Unicamp-1994) a) Faça o gráfico da função y = (L)nx com domínio x > 0.
b) A partir desse gráfico, faça o gráfico de y = f(x) = (L)n (-x), com domínio x < 0.
c) Explique como a função y = g(x) = (L)n(1 - x) está relacionada com a função f e obtenha o gráfico de g a partir do gráfico de f.

resposta:a) e b) Observe os gráficos a seguir: (imagem abaixo)
c) Sendo f(x) = (L)n (-x) e g(x) = (L)n (1 - x), o gráfico de g está "deslocado" uma unidade para a direita em relação ao gráfico de f, como é mostrado na figura anterior.

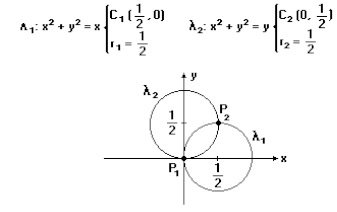
(Unicamp-1994) a) Identifique as circunferências de equações x² + y² = x e x² + y² = y, calculando o raio e o centro das mesmas. Esboce seus gráficos.
b) Determine os pontos de intersecção dessas circunferências e mostre que as retas a elas tangentes em cada um desses pontos são perpendiculares entre si.

resposta:a) Observe a figura: (imagem abaixo)
b) Um ponto de intersecção é (0,0) e as retas tangentes às respectivas circunferências por este ponto são x = 0 e y = 0, que são perpendiculares.
O outro ponto de intersecção é (1/2, 1/2) e as retas tangentes às respectivas circunferências por este ponto são y = 1/2 e x = 1/2 que são perpendiculares.

(Unicamp-1994) Seja α ≠ -1 um número complexo tal que αⁿ = 1, onde n é um número inteiro positivo. Prove que, se n for par, a expressão 1 - α + α² - α³ + ... + (-α)ⁿ é igual a 1; e, se n for ímpar, essa expressão é igual a (1 - α)/(1 + α).

resposta:S = 1 - α + α² - α³ + ... + (-α)ⁿ, αⁿ = 1, α ≠ -1 e
n

IN

S é a soma dos (n + 1) primeiros termos de uma progressão geométrica de 1(0). termo a1 = 1 e razão g = -α. Assim:

S = a1 (1 - qⁿ⁺¹) / (1 - q) =
= 1 [1 - (-α)ⁿ⁺¹] / [1 - (-α) ] =
= [1 - (- α) . (- α)ⁿ] / (1 + α) =
= [1 + α (-α)ⁿ] / (1 + α)

Se n é par, temos (-α)ⁿ = αⁿ = 1 e assim:
S = 1
Se n é ímpar, temos (-α)ⁿ = -αⁿ = -1 e assim:
S = (1 - α) / (1 + α)

(Unicamp-1994) Dada uma seqüência qualquer a(zero) . a1 . a2,..., a_n tem-se:

#(aŒ÷ - aŒ) = (a(zero) - a1) + (a1 - a‚) + ... + (a_n÷ -a_n) = a(zero) -a_n

No caso em que aŒ = j³, essa identidade assume a forma:

#[(j - 1)³ -j³] = 0³ -n³ = -n³

Use esta identidade para mostrar que:

#j² = 1² + 2² + ... + n² = (n³/3) + (n²/2) + (n/6)

resposta:# [(j - 1)³ - j³] = - n³ e
(j - 1)³ - j³ = -3j² + 3j - 1

Daí: # (-3j² + 3j - 1) = -n³

Assim sendo, para j = 1, 2, 3, 4, ... , n temos:

(-3.1²+3.1-1) + (-3.2²+3.2-1) + (-3.3²+3.3-1) + ...
... + (-3n²+3n-1) = -n³

-3(1²+2²+3²+...+n²) + 3(1+2+3+...+n) +
+ (-1-1-1... -1) = -n³

3(1²+2²+3²+...+n²)=n³+3(1+2+3+...+n)-n

3(1²+2²+3²+....+n²)=n³+ [3(1+n)n/2]-n

3(1²+2²+3²+...+n²)=n³+(3n²/2)+(3n/2)-n

3(1²+2²+3²+...+n²)=n³+(3n²/2)+(n/2)

1²+2²+3²+...+n²=(n³/3)+(n²/2)+(n/6)

(Unicamp-1994) a) Se a1 é um valor aproximado por excesso da raiz quadrada de um número inteiro N > 1, isto é, a1 > √N, mostre que N/a1 é valor aproximado por falta da mesma raiz, ou seja, N/a1 < √N.
b) Mostre que a média aritmética a‚ entre a1 e N/a1 também é uma aproximação de √N por excesso, isto é, a‚-√N > 0.
c) Mostre que a‚ é uma aproximação de √N melhor do que a1, isto é, √N < a‚ < a1. Mais do que isto, mostre que a‚-√N < (a1-√N)/2, vale dizer, o erro que se comete aproximando √N por a‚ é menor do que a metade do erro da aproximação anterior.

resposta:a) N/a1 = √N/a1 . √N < √N/a1 . a1 = √N, pois √N < a1 e portanto N/a1 < √N

b) (a1 - √N) / 2a1 > 0 Ì (a1 + N/a1)/2 - √N > 0
Ì a‚ - N > 0

c) 1) a‚ = (a1 + N/a1)/2 = (a1² + N)/2a1 < (a1² + a1²)/2a1² = a, e portanto a‚ < a1 como a‚ > √N tem-se √N < a‚ < a1

N/a1 < √N Ì a1 + N/a1 < a1 + √N
2a‚ < a1 + √N
2a‚ - 2√N < a1 - √N
a‚ - √N < a1 - √N/2

(Unicamp-1994) Em uma pirâmide de base quadrada, as faces laterais são triângulos eqüiláteros e todas as oito arestas são iguais a 1.
a) Calcule a altura e o volume da pirâmide.
b) Mostre que a esfera centrada no centro da base da pirâmide, e que tangencia as arestas da base, também tangencia as arestas laterais.
c) Calcule o raio do círculo intersecção da esfera com cada face lateral da pirâmide.

resposta:a) h = (√2)/2, v = (√2)/6

b) Sendo r o raio da esfera de centro O, que tangencia as arestas da base e r o raio da esfera de centro O, que tangencia as arestas laterais da pirâmide, tem-se:

1(0).) r é o apótema de um quadrado de lado 1.
Assim: 2r = 1 √ r = 1/2 (I)

2(0).) r é a altura relativa à hipotenusa do triângulo retângulo, cujos catetos são a altura da pirâmide e metade da diagonal da base e a hipotenusa e a aresta lateral da pirâmide. Assim:

hip. OH = cat . cat
1 . r = √2/2 . √2/2 √ r = 1/2 (II)

De (I) e (II) conclui-se que a esfera centrada em O, que tangencia as arestas da base da pirâmide, também tangencia as arestas laterais dessa pirâmide.

c) (√3)/6

(Unicamp-1992) O IBGE contratou um certo número de entrevistadores para realizar o recenseamento em uma cidade. Se cada um deles recenseasse 100 residências, 60 delas não seriam visitadas. Como, no entanto, todas as residências foram visitadas e cada recenseador visitou 102, quantas residências tem a cidade≠

resposta:3060 residências

(Unicamp-1992) Um vendedor propõe a um comprador de um determinado produto as seguintes alternativas de pagamento:
a) Pagamento à vista com 65% de desconto sobre o preço da tabela.
b) Pagamento em 30 dias com desconto de 55% sobre o preço de tabela.
Qual das duas alternativas é mais vantajosa para o comprador, considerando-se que ele consegue, com uma aplicação de 30 dias, um rendimento de 25%≠

resposta:Condição A
P

{0,35 P pago
þ
ÿ0,65 P desconto √ 0,65P.1,25 = 0,8125 P

Condição B
1,25 P =

{0,45 P pago
þ
ÿ0,55 P desconto √ 1,25 P - 0,45 P = 0,80 P portanto a primeira alternativa é mais vantajosa.