Questões de matemática

Tópicos de Vetores

(Cesgranrio-1994) ABCD é um quadrado. O vetor a seguir que indica a operação é igual a:

resposta:[A]

(Unirio-1995) São dados os pontos O (0, 0, 0) e A (1, 0, 2). O produto vetorial OAxOC, onde C é centro da esfera (x - 2)² + (y - 1)² + z² = 10, é o vetor:
a) (-2, 4, 1)
b) (-2, -4, 1)
c) (2, 0, 0)
d) (1, 1, -2)
e) (1, -1, 2)

resposta:[A]

(Cesgranrio-1993) O ângulo entre os vetores u=3i+j e v=i+2j é igual a:
a) 0°
b) 30°
c) 45°
d) 60°
e) 90°

resposta:[C]

(outros) Dados A = {-10, 0, 1, 10} e B = {100, 0, 1, 100}, determine a relação R de A em B formada pelos pares ordenados em que o 2(0). termo é igual ao quadrado do 1(0). termo.

resposta:y = x²

(Cesgranrio-1992) O módulo do vetor 2i - 3j + 6k vale:
a) 5
b) 7
c) 9
d) 11
e) 13

resposta:[B]

(Cesgranrio-1998) O menor valor do parâmetro K para o qual os vetores a(2, 1, 0), v(1, K, 4) e g(3, 1, -4K) são coplanares é:
a) -1
b) -1/2
c) 0
d) 1/2
e) 1

resposta:[B]

(Cesgranrio-1997) Os vetores @ (x, 2x - 1) e « (-2, 4) são ortogonais. Então o valor de x é igual a:
a) -3/2
b) -2/3
c) 2/5
d) 2/3
e) 3/2

resposta:[D]

(Unirio-1998) O ângulo formado pelos vetores u = (3,0) e v=(-2,2√3) mede:
a) 210°
b) 150°
c) 120°
d) 60°
e) 30°

resposta:[C]

(Unirio-1998) Determine se os pontos A(5, -1, 0), B (0, 2, 4), C(-3, 0, 6) e D (5, 2, 6) são coplanares ou não. Justifique a sua resposta.

resposta:Para que os pontos dados sejam coplanares, os vetores AB, AC e AD devem ser coplanares. Isto é, (AB, AC, AD) = 0.
Como AB = (-5, 3, 4), AC = (-8, 1, 6), AD = (0, 3, 6) e (AB, AC, AD) = 108 ≠ 0, os pontos A, B, C e D não são coplanares.

(Uerj-1998) As contas correntes de um banco são codificadas através de um número seqüencial seguido de um dígito controlador. Esse dígito controlador é calculado conforme o procedimento a seguir: (imagem abaixo)
A conta 643-5, aberta na década de 80, foi cadastrada no ano de:
a) 1985
b) 1986
c) 1987
d) 1988

resposta:[B]

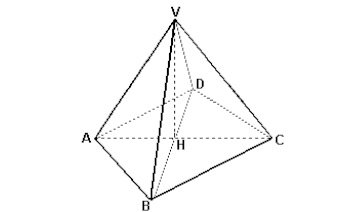
(Uerj-1998) A figura do R³ a seguir representa uma pirâmide de base quadrada ABCD em que as coordenadas são A (0,0,0), B (4,2,4) e C (0,6,6), e o vértice V é eqüidistante dos demais. (imagem abaixo)
A partir da análise dos dados fornecidos, determine:
a) as coordenadas do vértice D e a medida de cada aresta de base;
b) as coordenadas cartesianas do ponto V, considerando que o volume da pirâmide é igual a 72.

resposta:a) D = (-4, 4, 2). Medida de cada lado = 6
b) V = (-2, -4, 4) ou V = (2, 4, -4)

(Unirio-1999) Considere os vetores ¼=(√3, 5/2) e «=(-√3,1/2). A secante do ângulo formado pelos vetores ¼+« e ¼-« é:
a) 2
b) √2
c) 2√3 / 3
d) 1 / 2
e) -2

resposta:[A]

(Unirio-1999) Numa simulação em computador, onde o planeta Terra é representado por uma esfera de equação x² + y² + z² = 100, trabalha-se com uma situação na qual um OVNI virtual explode no ponto P(10, -8, 2√23). Nessa simulação, a altitude relativa à superfície terrestre em que o objeto voador não identificado explodiu foi de:
a) 6
b) 11
c) 16
d) 20
e) 23

resposta:[A]

(Uff-1999) Os vetores @ = (2, 1, 0), « = (0, 1, 2) e ¼ = (x, y,z) são tais que @ x « é perpendicular a ¼.
A relação entre x, y e z é:
a) 2x + y - z = 0
b) 2x - 2y + z = 0
c) x - 2y + z = 0
d) x + 2y - 2z = 0
e) x - 2y - z = 0

resposta:[C]

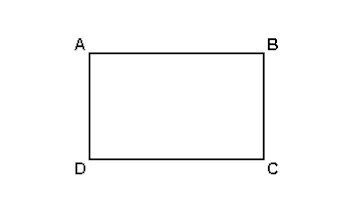
(Uff-1999) Considere o retângulo ABCD de dimensões BC = 3 m e Cî = 4 m. (imagem abaixo)
Calcule ¦¦ AB + BD + DC ¦¦

resposta:¦¦AC¦¦ = 5 m

(Ufrj-2000) Sejam O = (0, 0), P = (5, 2) e P = (2, 5).
Girando em torno de O, no sentido trigonométrico (anti-horário), o segmento OP de um certo ângulo &teta;, o ponto P transforma-se no ponto P .

Determine cos&teta;.

resposta:cos&teta; = 20/29

(Uff-2000) Em um retângulo ABCD, M e N são, respectivamente, os pontos médios dos lados AB e Cî. Tem-se que o vetor BM=(√3,1) e o vetor BN=(2√3,-2).
Determine o perímetro do retângulo.

resposta:Perímetro = 8+4√3 u.c.

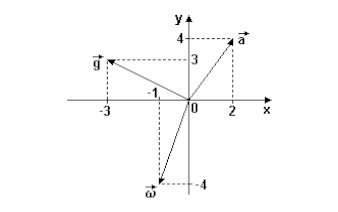
(Unirio-2000) (imagem abaixo) Considere os vetores a, g e Ÿ anteriormente representados. O vetor v tal que v = 1/2 a + g -1/4 Ÿ é:
a) (-6, 7/4)
b) (-2, 3)
c) (-7/4, 6)
d) (7/4, -6)
e) (6, -7/4)

resposta:[C]

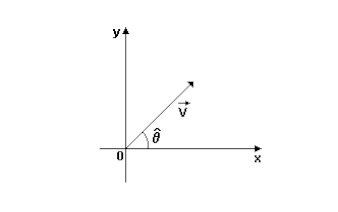
(Unirio-2000) (imagem abaixo) Considere um vetor « anteriormente representado. Sabendo-se que o módulo de « é 4 e que &teta;=π(Pi)/3, determine:

a) as coordenadas cartesianas de «;

b) um vetor ortogonal ao vetor « e de mesmo módulo que «.

resposta:a) « (2, 2√3)

b) (-2√3, 2) ou (2√3, -2)