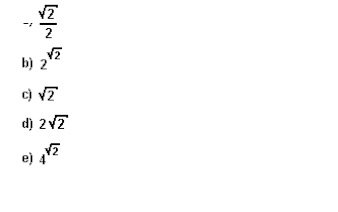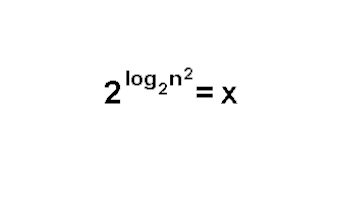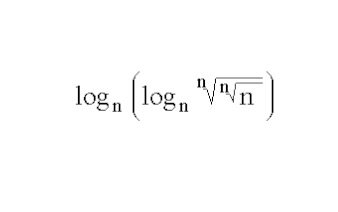Questões de matemática
Tópicos de Logarítmos
(Unesp-1994) Considere a função f, definida por f(x) = log
nx. Se f(n) = m e f(n + 2) = m + 1, os valores respectivos de n e m são:
a) 2 e 1.
b) 2 e 2.
c) 3 e 1.
d) 3 e 2.
e) 4 e 1.
resposta:[A]
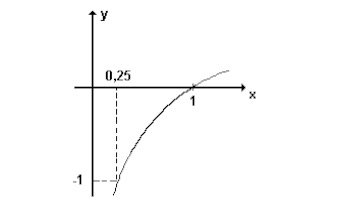
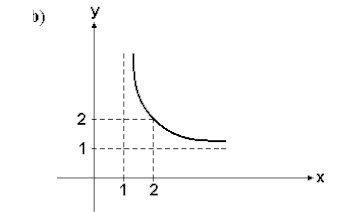
(Fuvest-1995) A figura a seguir mostra o gráfico da função logaritmo na base b.
O valor de b é:
(imagem abaixo)
a) 1/4.
b) 2.
c) 3.
d) 4.
e) 10.
resposta:[D]
(Fuvest-1995) O número x >1 tal que logÖ2 = log4x é:
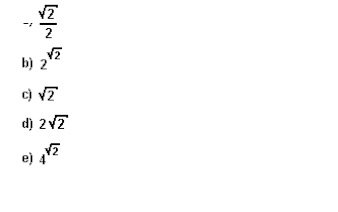resposta:[B]
(Ita-1995) Se x é um número real positivo, com x ≠ 1 e x ≠ 1/3, satisfazendo:
(2 + log3x) / (logÖø‚x) - (logÖ(x + 2)) / (1 + log3x) = logÖ(x + 2)
então x pertence ao intervalo I, onde:
a) I = (0, 1/9)
b) I = (0, 1/3)
c) I = (1/2, 1)
d) I = (1, 3/2)
e) I = (3/2, 2)
resposta:[B]
(Unesp-1995) Se a equação x² - b . x + 100 = 0 tem duas raízes reais n e t, n > 0 e t > 0, prove que:
log(zero)(n.t)
n + log(zero)(n.t) = 2b.
resposta:Se as raízes são n e t, então n + t = b e n.t = 100.
Assim:
log(zero)(n.t)
n + log(zero)(n.t) =
= log(zero)(10²)
n + log(zero)(10²) =
= log(zero)10²
n + log(zero)10² =
= 2nlog(zero) + 2tog(zero)10 =
= 2n + 2t = 2(n+t) = 2b
(Unitau-1995) Se
(imagem abaixo)
Então o(s) valor(es) real(is) de N que satisfaz(em) ײ - × = 0 é(são):
a) 0 e 1.
b) 1.
c) 0.
d) 0 e -1.
e) -1 e 1.
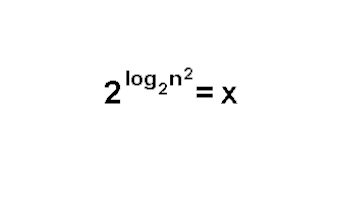resposta:[E]
(Unitau-1995) O domínio da função y = logÖ (2x - 1) é:
a) x > 1/2.
b) x > 0.
c) x < 1/2 e x ≠ 1.
d) x > 1/2 e x ≠ 1.
e) x ≠ 1/2.
resposta:[D]
(Fuvest-1990) Pressionando a tecla Log de uma calculadora, aparece no visor o logaritmo decimal do número que estava antes no visor. Digita-se inicialmente o número 88888888 (oito oitos). Quantas vezes a tecla Log precisa ser pressionada para que apareça mensagem de erro≠
a) 2.
b) 4.
c) 6.
d) 8.
e) 10.
resposta:[B]
(Fuvest-1991) A intensidade I de um terremoto, medida na escala Richter, é um número que varia de I = 0 até I = 8,9 para o maior terremoto conhecido. I é dado pela fórmula:
I = (2/3)log(zero)(E/E(zero))
onde E é a energia liberada no terremoto em quilowatt-hora e E(zero) = 7 × 10³ kWh.
a) Qual a energia liberada num terremoto de intensidade 8 na escala Richter≠
b) Aumentando de uma unidade a intensidade do terremoto, por quanto fica multiplicada a energia liberada≠
resposta:a) E = 7 . 10ª kWh
b) 10 √10
(Unesp-1991) Seja n > 0, n ≠ 1, um número real. Dada a relação
(n
y)/(1 + n
y) = x
determinar y em função de x e o domínio da função assim definida.
resposta:y = log
n (1-x)/x
Df = ]0,1[
(Fuvest-1992) Seja x=2
1(0)(0)(0). Sabendo que log(zero)2 é aproximadamente igual a 0,30103 pode-se afirmar que o número de algarismos de x é:
a) 300
b) 301
c) 302
d) 1000
e) 2000
resposta:[C]
(Unesp-1992) Seja x um número real, 16 < x < 81. Então:
a) log3x < log2x
b) log2x < log3x
c) logÖ2 = logÖ3
d) log2x³ = 1
e) log3x² = 10
resposta:[A]
(Fuvest-1993) Sabendo-se que 5
n = 2, podemos concluir que log2100 é igual a:
a) 2/n
b) 2n
c) 2 + n²
d) 2 + 2n
e) (2 + 2n)/n
resposta:[E]
(Fuvest-1993) Considere as equações:
I. log(x + y) = log x + log y
II. x + y = xy
a) As equações I e II têm as mesmas soluções≠ Justifique.
b) Esboce o gráfico da curva formada pelas soluções de I.
resposta:a) As equações I e II não têm as mesmas soluções.
(Unicamp-1993) Calcule o valor da expressão a seguir, onde n é um número inteiro, n≥2. Ao fazer o cálculo, você verá que esse valor é um número que não depende de n.
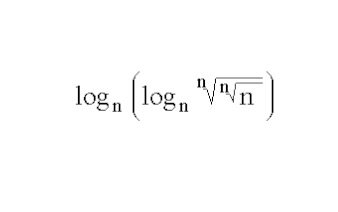resposta:-2
(Unesp-1993) Seja n > 0, n ≠ 1, um número real. Se log
nx = 3 log(zero)x para todo número real x > 0, x ≠ 1, então:
a) n = 3
b) n = 10/3
c) n = 30
d) n = ³√10
e) n = 10³
resposta:[D]
(Cesgranrio-1995) Se log(zero) 123 = 2,09, o valor de log(zero) 1,23 é:
a) 0,0209
b) 0,09
c) 0,209
d) 1,09
e) 1,209
resposta:[B]
(Fuvest-1996) Seja f(x) o logaritmo de 2x na base x² + (1/2).
a) Resolva a equação f(x) = 1/2.
b) Resolva a inequação f(x) > 1.
resposta:a) V = {√6/6}
b) V = ]0; (2-√2)/2[ » ]√2/2; (2+√2)/2[
(Cesgranrio-1994) Se log √(a) = 1,236, então o valor de log ³√(a) é:
a) 0,236
b) 0,824
c) 1,354
d) 1,854
e) 2,236
resposta:[B]
próxima »
