Questões de matemática
Tópicos de Progressão Geométrica
(Unicamp-1994) Seja α ≠ -1 um número complexo tal que α
n = 1, onde n é um número inteiro positivo. Prove que, se n for par, a expressão 1 - α + α² - α³ + ... + (-α)
n é igual a 1; e, se n for ímpar, essa expressão é igual a (1 - α)/(1 + α).
resposta:S = 1 - α + α² - α³ + ... + (-α)
n, α
n = 1, α ≠ -1 e
n

IN
S é a soma dos (n + 1) primeiros termos de uma progressão geométrica de 1(0). termo a1 = 1 e razão g = -α. Assim:
S = a1 (1 - q
n+1) / (1 - q) =
= 1 [1 - (-α)
n+1] / [1 - (-α) ] =
= [1 - (- α) . (- α)
n] / (1 + α) =
= [1 + α (-α)
n] / (1 + α)
Se n é par, temos (-α)
n = α
n = 1 e assim:
S = 1
Se n é ímpar, temos (-α)
n = -α
n = -1 e assim:
S = (1 - α) / (1 + α)
(Ita-1995) Se a soma dos termos da progressão geométrica dada por 0,3: 0,03: 0,003:... é igual ao termo médio de uma progressão aritmética de três termos, então a soma dos termos da progressão aritmética vale:
a) 1/3
b) 2/3
c) 1
d) 2
e) 1/2
resposta:[C]
(Pucsp-1995) Sabe-se que a seqüência (1/3, a, 27), na qual a > 0, é uma progressão geométrica e a seqüência (x, y, z), na qual x + y + z = 15, é uma progressão aritmética. Se as duas progressões têm razões iguais, então:
a) x = - 4.
b) y = 6.
c) z = 12.
d) x = 2y.
e) y = 3x.
resposta:[A]
(Unesp-1995) A seqüência de números reais a, b, c, d forma, nessa ordem, uma progressão aritmética cuja soma dos termos é 110; a seqüência de números reais a, b, e, f forma, nessa ordem, uma progressão geométrica de razão 2. A soma d + f é igual a:
a) 96.
b) 102.
c) 120.
d) 132.
e) 142.
resposta:[D]
(Unesp-1994) Sejam a, b e c três números reais estritamente positivos e tais que a < b + c. Se a, b, c formam, nessa ordem, uma progressão geométrica de razão q, prove que:
a) q² + q - 1 > 0;
b) q > ( - 1 + √5)/2.
resposta:a) a, b, e c formam uma PG de razão q, daí temos:
a
0. Como a  IR*ø conclui-se que: q²+q-1>0.
IR*ø conclui-se que: q²+q-1>0.
b) q²+q-1>0 e q >0Ì (-1+ √5)/2
(Unitau-1995) Em um freezer de hospital existem 50 frascos de sangue tipo A e 81 frascos tipo B. Dele são retirados 2 frascos, um após o outro, sem reposição. O primeiro frasco retirado foi tipo B. A probabilidade de que o segundo frasco seja A é:
a) 5/130.
b) 5/13.
c) 81/131.
d) 50/131.
e) 1/10.
resposta:[B]
(Unitau-1995) A soma dos termos da seqüência (1/2;1/3;2/9;4/27;...) é:
a) 15 × 101.
b) -3 × 101.
c) 15 × 10².
d) 5 × 101.
e) 3/5.
resposta:[A]
(Unitau-1995) O valor da soma: S = 4 + (1/10) + [36/10³ + 36/10¦ + 36/107 + 36/10ª +...] é igual a:
a) 99/22.
b) 91/22.
c) 91/21.
d) 90/21.
e) 81/23.
resposta:[B]
(Fuvest-1990) Um país contraiu em 1829 um empréstimo de 1 milhão de dólares, para pagar em cem anos, à taxa de juros de 9% ao ano. Por problemas de balança comercial, nada foi pago até hoje, e a dívida foi sendo "rolada", com capitalização anual dos juros. Qual dos valores a seguir está mais próximo do valor da dívida em 1989≠
Para os cálculos adote (1,09)≅ 2.
a) 14 milhões de dólares.
b) 500 milhões de dólares.
c) 1 bilhão de dólares.
d) 80 bilhões de dólares.
e) 1 trilhão de dólares.
resposta:[E]
(Unicamp-1991) Existem 4 números inteiros positivos e consecutivos tais que o produto de 2 deles seja igual ao produto dos outros dois≠ Justifique.
resposta:Não. Ao escolher 4 números inteiros positivos e consecutivos, teremos sempre 2 pares e 2 ímpares, logo os possíveis produtos são:
(I) (n(0). par) x (n(0). par) ≠ (n(0). ímpar) x (n(0). ímpar)
O 1(0). membro tem resultado par e o 2(0). membro tem resultado ímpar.
(II) (n(0). par) x (n(0). ímpar) ≠ (n(0). par) x (n(0). ímpar)
Os fatores que compõem o 1(0). membro são diferentes dos fatores que compõem o 2(0). membro.
(Unicamp-1991) Começando com um cilindro de raio 1 e altura também 1, define-se o procedimento de colocar sobre um cilindro anterior um outro cilindro de igual altura e raio 2/3 do raio anterior.
Embora a altura do sólido fictício resultante seja infinita, seu volume pode ser calculado. Faça esse cálculo.
resposta:Observe a figura a seguir:

(Unicamp-1991) Considere que certo país troca de moeda cada vez que a inflação acumulada atinge a cifra de 900%. A nova moeda vale sempre 1000 vezes a antiga. Com uma inflação de 25% ao mês, em quantos meses esse país trocará de moeda≠
Use log(zero) 2 = 0,301.
resposta:Observe a figura a seguir:

(Fuvest-gv-1991) Dado um quadrado Q cujo lado tem comprimento (L)=1, considere a seqüência infinita de quadrados {Q,Q‚,Q3,...} onde cada quadrado é obtido unindo-se os pontos médios dos lados do quadrado anterior. A soma das áreas de todos os quadrados da seqüência é:
a) 4
b) (4√2)/(√2-1)
c) 4/3
d) 2
e) √2/(√2-1)
resposta:[D]
(Unesp-1992) Um ângulo de 69°20 é dividido em dois ao meio. A seguir, um dos ângulos obtidos também é dividido em dois ao meio. E assim por diante. Se este processo é interrompido quando se obtém um ângulo 1°5 , determinar o número de divisões efetuadas.
resposta:6
(Fuvest-1993) Uma progressão geométrica tem primeiro termo igual a 1 e razão igual a √2. Se o produto dos termos dessa progressão é 2³ª, então o número de termos é igual a:
a) 12
b) 13
c) 14
d) 15
e) 16
resposta:[B]
(Unesp-1993) Os comprimentos das circunferências de uma seqüência de círculos concêntricos formam uma progressão aritmética de razão 2. Os raios desses círculos formam uma:
a) progressão geométrica de razão 1/2.
b) progressão geométrica de razão 1/π(Pi).
c) progressão aritmética de razão 2.
d) progressão aritmética de razão π(Pi).
e) progressão aritmética de razão 1/π(Pi).
resposta:[E]
(Ufpr-1995) Considere as progressões geométricas nas quais an indica o n-ésimo termo, sendo a3 = 8 e a5 = 32. É correto afirmar que:
01) A razão de cada uma dessas progressões é 4.
02) Todos os termos dessas progressões são necessariamente positivos.
04) O primeiro termo de cada uma dessas progressões é 1.
08) Se i > 0 é a razão de uma das progressões geométricas, os números log‹ a1, log‹ a3, log‹ a5 formam, nesta ordem, uma progressão aritmética.
resposta:8
(Cesgranrio-1994) A população de certa cidade é, hoje, igual a P(zero) e cresce 2% ao ano. A população dessa cidade daqui a n anos será:
a) P(zero)(1 + n/50)
b) P(zero)(1 + (n - 1)/50)
c) P(zero) + (n - 1)/50
d) P(zero) . 1,02n1
e) P(zero) . 1,02n
resposta:[E]
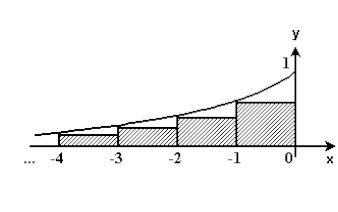
(Ufes-1996) A figura a seguir representa o gráfico da função y = 2x , x ≤ 0, e os primeiros elementos de uma seqüência infinita de retângulos.
A soma das áreas de todos os retângulos dessa seqüência infinita é:
(imagem abaixo)
Dado: (ua = unidade de área)
a) 1/2 ua
b) 1 ua
c) 3/2 ua
d) 2 ua
e) maior que 2 ua
resposta:[B]
próxima »



