Questões de matemática

Tópicos de Geometria Analítica

(Fuvest-1994) Fixado o ponto N = (0, 1), a cada ponto P do eixo das abscissas associamos o ponto P ≠ N obtido pela intersecção da reta PN com a circunferência x² + y² = 1.
a) Que pontos do eixo das abscissas foram associados aos pontos (x, y) da circunferência, com y < 0≠
b) Quais as coordenadas do ponto P da circunferência, associado a P = (c, 0), c ≠ 0≠

resposta:a) P (a, 0)/-1 < a <1

b) P [2c/(c²+1); (c²-1)/(c²+1)]

(Unesp-1994) Seja A a intersecção das retas r, de equação y = 2x, e s, de equação y = 4x - 2. Se B e C são as intersecções respectivas dessas retas com o eixo das abscissas, a área do triângulo ABC é:
a) 1/2.
b) 1.
c) 2.
d) 3.
e) 4.

resposta:[A]

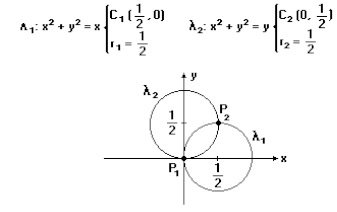
(Unicamp-1994) a) Identifique as circunferências de equações x² + y² = x e x² + y² = y, calculando o raio e o centro das mesmas. Esboce seus gráficos.
b) Determine os pontos de intersecção dessas circunferências e mostre que as retas a elas tangentes em cada um desses pontos são perpendiculares entre si.

resposta:a) Observe a figura: (imagem abaixo)
b) Um ponto de intersecção é (0,0) e as retas tangentes às respectivas circunferências por este ponto são x = 0 e y = 0, que são perpendiculares.
O outro ponto de intersecção é (1/2, 1/2) e as retas tangentes às respectivas circunferências por este ponto são y = 1/2 e x = 1/2 que são perpendiculares.

(Fuvest-1995) Sejam A = (1, 2) e B = (3, 2) dois pontos do plano cartesiano. Nesse plano, o segmento AC é obtido do segmento AB por uma rotação de 60°, no sentido anti-horário, em torno do ponto A.
As coordenadas do ponto C são:
a) (2, 2 + √3).
b) (1 + √3, 5/2).
c) (2, 1 + √3).
d) (2, 2 - √3).
e) (1 + √3, 2 + √3).

resposta:[A]

(Fuvest-1995) Uma circunferência de raio 2, localizada no primeiro quadrante, tangencia o eixo x e a reta de equação 4x - 3y = 0.
Então a abscissa do centro dessa circunferência é:
a) 1
b) 2
c) 3
d) 4
e) 5

resposta:[D]

(Ita-1995) Três pontos de coordenadas, respectivamente, (0, 0), (b, 2b) e (5b, 0), com b > 0, são vértices de um retângulo. As coordenadas do quarto vértice são dadas por:
a) (- b, - b)
b) b) (2b, - b)
c) (4b, - 2b)
d) (3b, - 2b)
e) (2b, - 2b)

resposta:[C]

(Ita-1995) Uma reta t do plano cartesiano xOy tem coeficiente angular 2a e tangencia a parábola y = x² - 1 no ponto de coordenadas (a, b). Se (c, 0) e (0, d) são as coordenadas de dois pontos de t tais que c > 0 e c = -2d, então a/b é igual a:
a) - 4/15
b) - 5/16
c) - 3/16
d) - 6/15
e) - 7/15

resposta:[A]

(Pucsp-1995) Os pontos A = (-1; 1), B = (2; -1) e C = (0; -4) são vértices consecutivos de um quadrado ABCD. A equação da reta suporte da diagonal Bî, desse quadrado, é:
a) x + 5y + 3 = 0.
b) x - 2y - 4 = 0.
c) x - 5y - 7 = 0.
d) x + 2y - 3 = 0.
e) x - 3y - 5 = 0.

resposta:[C]

(Unesp-1995) Considere o quadrado de lados paralelos aos eixos coordenados e circunscrito à circunferência de equação:

x² + y² - 6x - 4y + 12 = 0.

Determine as equações das retas que contêm as diagonais desse quadrado.

resposta:y = x - 1 e y = -x + 5

(Fuvest-1995) Sejam A = (0, 0), B = (0, 5) e C = (4, 3) pontos do plano cartesiano.
a) Determine o coeficiente angular da reta BC.
b) Determine a equação da mediatriz do segmento BC. O ponto A pertence a esta mediatriz≠
c) Considere a circunferência que passa por A, B e C. Determine a equação da reta tangente a esta circunferência no ponto A.

resposta:a) m = -1/2
b) y = 2x e o ponto A pertence à mediatriz
c) y = -x/2

(Unicamp-1995) Em um sistema de coordenadas ortogonais no plano são dados o ponto (5, -6) e o círculo x² + y² = 25. A partir do ponto (5,-6), traçam-se duas tangentes ao círculo. Faça uma figura representativa desta situação e calcule o comprimento da corda que une os pontos de tangência.

resposta:A corda mede (60 √61)/61 unidades de comprimento

(Unesp-1995) Dado um sistema de coordenadas cartesianas no plano, considere os pontos A(2, 2), B(4, -1) e C(m, 0). Para que AC + CB seja mínimo, o valor de m deve ser:
a) 7/3.
b) 8/3.
c) 10/3.
d) 3,5.
e) 11/3.

resposta:[C]

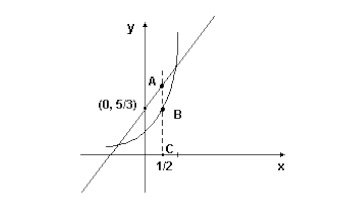
(Unesp-1994) A figura adiante mostra os gráficos de uma função exponencial y = a^x e da reta que passa pelo ponto (0, 5/3) e tem inclinação 10/7. Pelo ponto C = (1/2, 0) passou-se a perpendicular ao eixo x, que corta os gráficos, respectivamente, em B e A. (imagem abaixo)
Supondo-se que B esteja entre A e C, conforme mostra a figura, e que a medida do segmento AB é dada por 8/21, determine o valor de a.

resposta:4

(Unesp-1994) Num sistema de coordenadas cartesianas retangulares de origem 0, considere os pontos A = (3, 0), B = (3, 5) e C = (0, 5). Seja r a reta pelo ponto M = (1, 2) e que corta OC e AB em Q e P, respectivamente, de modo que a área do trapézio OQPA seja metade da do quadrado OCBA. Determine a equação de r .

resposta:x -y +1 = 0

(Unitau-1995) A equação da reta que passa pelos pontos (3, 3) e (6, 6) é:
a) y = x.
b) y = 3x.
c) y = 6x.
d) 2y = x.
e) 6y = x.

resposta:[A]

(Unitau-1995) A reta r é perpendicular à bissetriz dos quadrantes pares e intercepta um eixo coordenado no ponto A(0, -1).
Escreva a equação geral da reta r.

resposta:x - y -1 = 0

(Fuvest-1990) A reta y = mx (m > 0) é tangente à circunferência (x - 4)² + y² = 4. Determine o seno do ângulo que a reta forma com o eixo x.
a) 1/5.
b) 1/2.
c) (√3)/2.
d) (√2)/2.
e) √5.

resposta:[B]

(Fuvest-1991) a) As extremidades de um diâmetro de uma circunferência são (-3, 1) e (5, -5). Determine a equação da circunferência.
b) Determine a equação da circunferência que passa pelo ponto (9, √3) e que é tangente às retas y = 0 e y = √3x.

resposta:a) (x - 1)² + (y + 2)² = 25

b) —: (x - 6)² + (y - 2√3)² = 12
—‚: (x - 14)² + (y - 14√3/3)² = 196/3

(Unicamp-1991) Um foguete com ogiva nuclear foi acidentalmente lançado de um ponto da Terra e cairá perigosamente de volta à Terra. Se a trajetória plana desse foguete segue o gráfico da equação y = -x² + 300x, com que inclinação se deve lançar outro foguete com trajetória retilínea, do mesmo ponto de lançamento, para que esse último intercepte e destrua o primeiro no ponto mais distante da Terra≠

resposta:α = arc tg 150