Questões de matemática
Tópicos de Geometria Espacial
(Fuvest-1994) A base de uma pirâmide regular é um quadrado ABCD de lado 6 e diagonais AC e BD. A distância de seu vértice E ao plano que contém a base é 4.
a) Determine o volume do tetraedro ABDE.
b) Determine a distância do ponto B ao plano que contém a face ADE.
resposta:a) 24 U. volume.
b) 4,8 U. comprimento.
(Unesp-1994) Num tonel de forma cilíndrica, está depositada uma quantidade de vinho que ocupa a metade de sua capacidade. Retirando-se 40 litros de seu conteúdo, a altura do nível do vinho baixa de 20%. O número que expressa a capacidade desse tonel, em litros é:
a) 200.
b) 300.
c) 400.
d) 500.
e) 800.
resposta:[C]
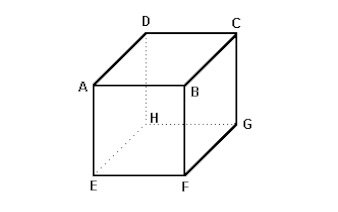
(Unesp-1994) Considere o cubo da figura adiante. Das alternativas a seguir, aquela correspondente a pares de vértices que determinam três retas, duas a duas reversas, é:
(imagem abaixo)
a) (A,D); (C,G); (E,H).
b) (A,E); (H,G); (B,F).
c) (A,H); (C,F); (F,H).
d) (A,E); (B,C); (D,H).
e) (A,D); (C,G); (E,F).
 resposta:
resposta:[E]
(Unicamp-1994) Em uma pirâmide de base quadrada, as faces laterais são triângulos eqüiláteros e todas as oito arestas são iguais a 1.
a) Calcule a altura e o volume da pirâmide.
b) Mostre que a esfera centrada no centro da base da pirâmide, e que tangencia as arestas da base, também tangencia as arestas laterais.
c) Calcule o raio do círculo intersecção da esfera com cada face lateral da pirâmide.
resposta:a) h = (√2)/2, v = (√2)/6
b) Sendo r o raio da esfera de centro O, que tangencia as arestas da base e r o raio da esfera de centro O, que tangencia as arestas laterais da pirâmide, tem-se:
1(0).) r é o apótema de um quadrado de lado 1.
Assim: 2r = 1 √ r = 1/2 (I)
2(0).) r é a altura relativa à hipotenusa do triângulo retângulo, cujos catetos são a altura da pirâmide e metade da diagonal da base e a hipotenusa e a aresta lateral da pirâmide. Assim:
hip. OH = cat . cat
1 . r = √2/2 . √2/2 √ r = 1/2 (II)
De (I) e (II) conclui-se que a esfera centrada em O, que tangencia as arestas da base da pirâmide, também tangencia as arestas laterais dessa pirâmide.
c) (√3)/6
(Unicamp-1995) Ao serem retirados 128 litros de água de uma caixa d água de forma cúbica, o nível da água baixa 20 centímetros.
a) Calcule o comprimento das arestas da referida caixa.
b) Calcule sua capacidade em litros (1 litro equivale a 1 decímetro cúbico).
resposta:a) a = 8 dm
b) V = 512 litros.
(Fuvest-1995) Uma superfície esférica de raio 13 cm é cortada por um plano situado a uma distância de 12 cm do centro da superfície esférica, determinando uma circunferência.
O raio desta circunferência, em cm é:
a) 1.
b) 2.
c) 3.
d) 4.
e) 5.
resposta:[E]
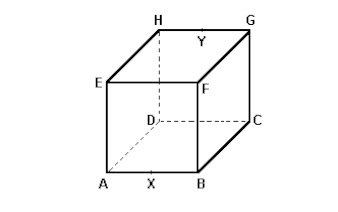
(Fuvest-1995) Na figura a seguir, X e Y são, respectivamente, os pontos médios das arestas AB e CD do cubo. A razão entre o volume do prisma AXFEDYGH e o do cubo é:
a) 3/8.
b) 1/2.
c) 2/3.
d) 3/4.
e) 5/6.
 resposta:
resposta:[D]
(Ita-1995) Um cone circular reto tem altura 12 cm e raio da base 5 cm. O raio da esfera inscrita neste cone mede, em cm:
a) 10/3
b) 7/4
c) 12/5
d) 3
e) 2
resposta:[A]
(Ita-1995) O raio de um cilindro de revolução mede 1,5 m. Sabe-se que a área da base do cilindro coincide com a área da secção determinada por um plano que contém o eixo do cilindro. Então, a área total do cilindro, em m², vale:
a) 3π(Pi)²/4
b) 9π(Pi)(2 + π(Pi))/4
c) π(Pi)(2 + π(Pi))
d) π(Pi)²/2
e) 3π(Pi)(π(Pi) + 1)/2
resposta:[B]
(Ita-1995) Dado um prisma hexagonal regular, sabe-se que sua altura mede 3 cm e que sua área lateral é o dobro da área de sua base. O volume deste prisma, em cm³, é:
a) 27√3
b) 13√2
c) 12
d) 54√3
e) 17√5
resposta:[D]
(Ita-1995) Dada uma pirâmide regular triangular, sabe-se que sua altura mede 3a cm, onde "a" é a medida da aresta de sua base. Então, a área total desta pirâmide, em cm², vale:
a) (a²√327)/4
b) (a²√109)/2
c) (a²√3)/2
d) [a²√3 . (2 + √33)]/2
e) [a²√3 . (1 + √109)]/4
resposta:[E]
(Pucsp-1995) A base de uma pirâmide reta é um quadrado cujo lado mede 8√2 cm. Se as arestas laterais da pirâmide medem 17 cm, o seu volume, em centímetros cúbicos, é:
a) 520.
b) 640.
c) 680.
d) 750.
e) 780.
resposta:[B]
(Unesp-1995) Uma piscina de forma retangular tem 8 m de largura, 15 m de comprimento, 0,9 m de profundidade num de seus extremos e 2,7 m de profundidade no outro extremo, sendo seu fundo um plano inclinado. Calcule o volume da água da piscina quando a altura do nível da água é de 0,6 m na extremidade mais funda.
resposta:12 m³ ou 12000 litros
(Fuvest-1995) No cubo de aresta a mostrado na figura adiante, X e Y são pontos médios das arestas AB e GH respectivamente. Considere a pirâmide de vértice F e cuja base é o quadrilátero XCYE. Calcule, em função de a,
a) o comprimento do segmento XY.
b) a área da base da pirâmide.
c) o volume da pirâmide.
 resposta:
resposta:a) a√2
b) (a²√6)/2
c) a³/3
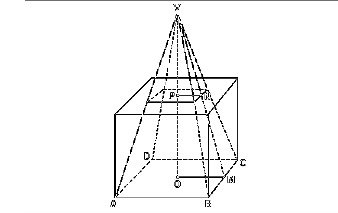
(Unicamp-1995) Uma pirâmide regular, de base quadrada, tem altura igual a 20 cm. Sobre a base dessa pirâmide constrói-se um cubo de modo que a face oposta à base do cubo corte a pirâmide em um quadrado de lado igual a 5 cm. Faça uma figura representativa dessa situação e calcule o volume do cubo.
resposta:Observe a figura
(imagem abaixo)
O volume do cubo é de 1000 cm³
(Unesp-1995) Entre todas as retas suportes das arestas de um certo cubo, considere duas, r e s, reversas. Seja t a perpendicular comum a r e a s. Então:
a) t é a reta suporte de uma das diagonais de uma das faces do cubo.
b) t é a reta suporte de uma das diagonais do cubo.
c) t é a reta suporte de uma das arestas do cubo.
d) t é a reta que passa pelos pontos médios das arestas contidas em r e s.
e) t é a reta perpendicular a duas faces do cubo, por seus pontos médios.
resposta:[C]
(Unesp-1994) Um produto é acondicionado em três tipos de embalagens cilíndricas, todas de mesma altura, mas de raios a, b e c, distintos entre si. Se a capacidade da embalagem de raio c é igual à soma da capacidade da embalagem de raio a com a de raio b , prove que c² = a² + b².
resposta:Sendo h a altura de cada embalagem cilíndrica, temos:
π(Pi)c²h = π(Pi)a²h Ì c² = a² + b²
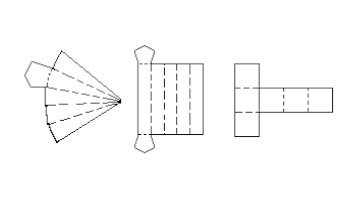
(Unitau-1995) Se dobrarmos convenientemente as linhas tracejadas das figuras a seguir, obteremos três modelos de figuras espaciais cujos nomes são:
(imagem abaixo)
a) tetraedro, octaedro e hexaedro.
b) paralelepípedo, tetraedro e octaedro.
c) octaedro, prisma e hexaedro.
d) pirâmide, tetraedro e hexaedro.
e) pirâmide pentagonal, prisma pentagonal e hexaedro.
 resposta:
resposta:[E]
(Unitau-1995) Uma esfera de raio R está inscrita em um cilindro. O volume do cilindro é igual a:
a) π(Pi)r³/3.
b) 2π(Pi)r³/3.
c) π(Pi)r³.
d) 2r³.
e) 2π(Pi)r³.
resposta:[E]
próxima »





